【杂文·I】Proof Automation with Large Language Models

这是一篇公式化论文，公式就是 LLM+XXX 不断迭代修复，同时说明自己发现的现象，以及如何让 LLM 通过 prompt engineering 的方式提高 XX 率。

摘要：诸如 Coq 之类的交互式定理证明器，是在形式上保证软件正确性的强大工具。然而，使用这些工具往往需要大量的人工投入与专业知识。尽管大型语言模型（LLMs）在自动生成自然语言形式的非正式证明方面已展现出潜力，但在生成可直接用于交互式定理证明器的形式化证明时，其表现仍不尽如人意。本文开展了一项形成性研究，以识别 LLM 在生成形式化证明过程中常见的错误。通过分析 GPT-3.5 在 520 个证明生成错误中的表现，我们发现 GPT-3.5 往往能够正确把握证明的高层结构，但在低层细节处理上存在明显不足。基于这一洞察，我们提出了 PALM——一种全新的“生成—修复”方法，该方法首先利用 LLM 生成初始证明，然后借助针对性的符号化方法迭代修复低层次问题。我们在一个包含超过 1 万个定理的大规模数据集上对 PALM 进行了评估。实验结果表明，PALM 显著优于其他最先进的方法，成功证明的定理数量提高了 76.6% 至 180.4%，并额外证明了 1270 个现有方法无法完成的定理。我们还展示了 PALM 在不同 LLM 间的可泛化性。

引言

正确性对于软件系统而言至关重要。交互式定理证明器（ITP），如 Coq、Isabelle 和 Lean，是为软件提供语义层面强保证的强大工具。在 ITP 中，用户可以针对程序陈述并证明形式化定理；这些证明将由 ITP 进行机械化检验，从而在根基层面提供关于其正确性的有力保证。这一策略已在多个应用领域中获得成功，包括编译器、分布式系统以及操作系统内核。然而，这种方法也存在代价，即用户必须提供一份证明脚本，以帮助 ITP 构建所需定理的证明。编写这些证明脚本可能需要巨大的投入。例如，验证 CompCert C 编译器就耗费了 6 人年时间，撰写了 100,000 行 Coq 证明脚本。

为减少 ITP 所需的人工投入，研究者提出了多种证明自动化技术，这些技术主要可分为两类：符号方法与机器学习方法。符号方法结合已建立的定理与外部自动定理证明器（ATP），如 Z3 和 CVC5，以自动化定理证明。尽管有效，但此类方法受限于无法执行高阶与归纳推理，因此难以证明复杂定理。机器学习方法则利用模型在启发式引导的搜索过程中预测下一步证明操作。这类方法虽不具备符号方法的局限，但却需要大量的训练数据。

近年来，预训练的大型语言模型（LLM）在生成非形式化的自然语言证明方面表现出潜力，这表明它们有望进一步改进现有的证明自动化方法。不幸的是，即便是最先进的 LLM，在一次性生成形式化证明方面依旧效率低下：在我们的评估中，GPT-3.5 仅能证明 3.7% 的定理，而 Llama-3-70b-Instruct 仅能证明 3.6%。为理解其原因，我们开展了一项形成性研究，分析了 GPT-3.5 在生成形式化证明时所犯的错误。在这项研究中，我们分析了 579 个不同复杂度的定理，并识别出七类错误。总体而言，我们发现 GPT-3.5 虽常能产出具备正确高层结构的证明，但在低层细节上往往出现偏差。令人鼓舞的是，我们还观察到，许多错误有潜力通过符号方法加以修复，包括基于启发式的搜索和证明修复。

LLM 的固有问题：高维会做，细节出问题

受此研究启发，我们提出了 PALM，这是一种结合 LLM 与符号方法的生成-修复新范式。我们的核心洞见在于：利用 LLM 生成一份初始证明，使其大概率具备正确的高层结构，随后借助针对性的符号方法迭代修复与具体证明步骤相关的低层问题。PALM 依赖于四种修复机制，它们针对我们在形成性研究中识别出的常见错误类型进行处理。若修复机制失效，PALM 将采用回溯程序以再生先前的证明步骤，从而尝试修复高层证明结构中的错误。尽管 PALM 的实现目标是 Coq，但其底层原理同样可推广至其他 ITP，例如 Isabelle 与 Lean。

为了评估我们方法的有效性，我们使用包含 10,842 个定理的 CoqGym 数据集进行了广泛的实验评估。结果表明，PALM 能够成功证明 40.4% 的定理，显著优于当前最先进的方法 Passport、Proverbot9001 和 Draft, Sketch, and Prove (DSP) ，它们分别仅能证明 14.4%、17.1% 和 22.9% 的定理。

此外，我们还进行了实验，以验证 PALM 各个组成部分的有效性，以及 PALM 在不同大语言模型上的泛化能力。总之，本文的贡献包括：

我们进行了一项形成性研究，总结了 GPT-3.5 在 Coq 中证明定理时常见的错误。
我们提出了 PALM，这是一种新颖的自动化证明方法，将大语言模型与符号方法结合在一个“生成-修复”流水线中。
我们在大规模数据集上评估了 PALM，并展示了它显著优于现有方法。

PALM 的源代码和可复现实验包已公开提供。

2 预备知识

2.1 Coq 中的交互式定理证明

Coq 证明助理是一款广受欢迎的工具，用于开发数学定理的机器检验证明以及验证复杂的软件系统。Coq 通过一组证明策略（proof tactics）帮助用户以交互方式构建证明。本节首先介绍 Coq 中交互式证明开发的基本概念，然后结合图 1 中的一个示例定理加以说明。

定理（Theorems）： 在 Coq 中，定理的定义通常以关键字 Theorem 或 Lemma 开始，随后给出定理名称及其陈述。图 1 展示了定理 add_comm，它说明自然数加法具有交换律。随后跟随的是证明脚本（proof script），即一系列策略的序列，用于解释如何构造该陈述的证明。证明脚本通常在交互式证明模式下开发。处理图 1 的首行时，Coq 将进入证明模式。在证明过程中，用户可以自由地复用先前已经证明的定理。

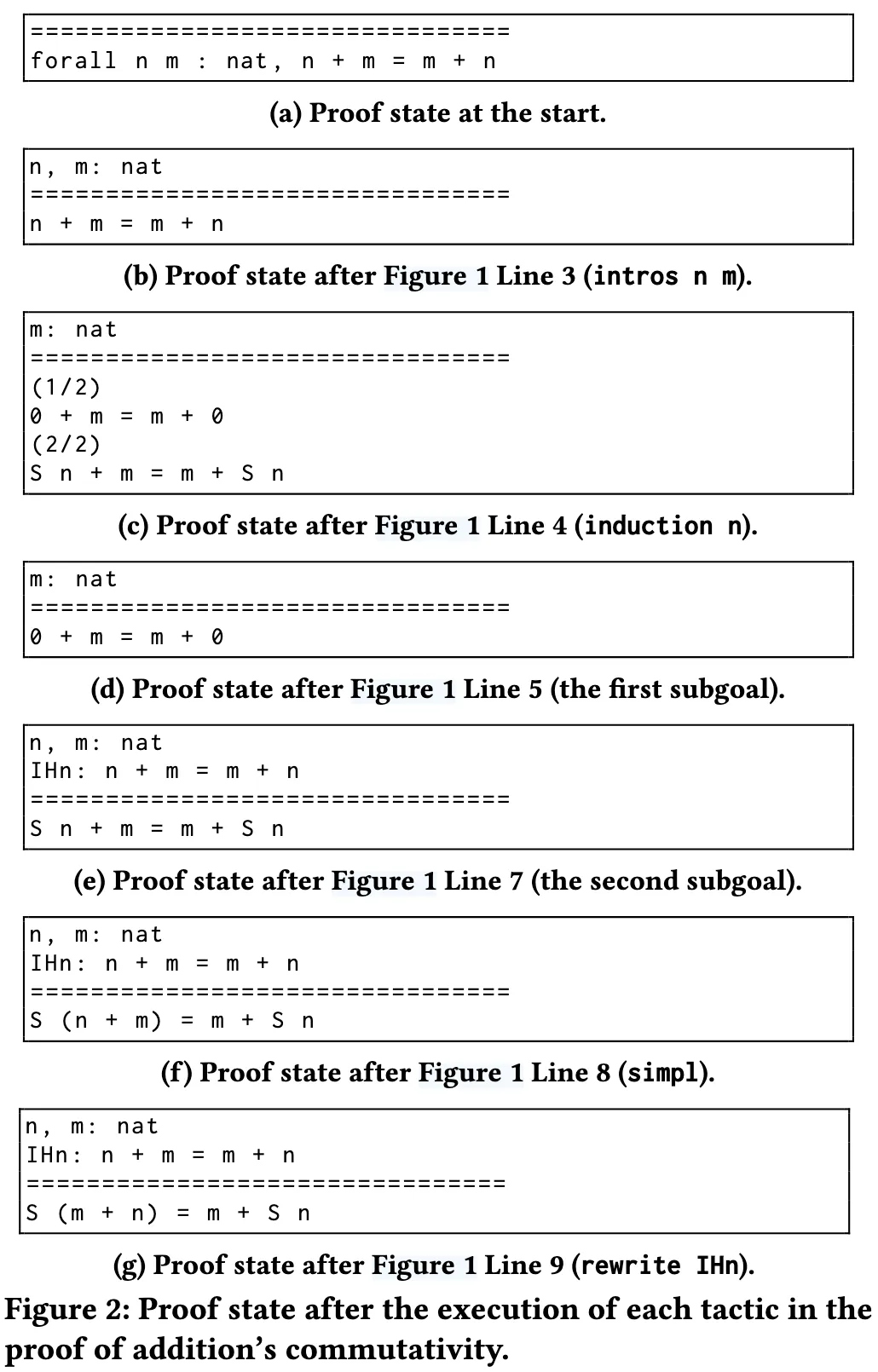
证明状态（Proof States）： 在证明模式下，Coq 的界面显示当前的证明状态，即尚未解决的目标列表。每个目标由一个局部上下文 (lc) 与一个未完成的证明义务 (st) 组成。局部上下文包含可用于证明 st 的假设与前提，这与已被证明的定理（作为全局上下文的一部分）是不同的。图 2 展示了 add_comm 证明过程中出现的中间证明状态：每个列表对应图 1 中某条策略执行后所显示的状态。根据 Coq 界面的约定，局部上下文显示在双横线上方，而当前的证明义务显示在双横线下方。

策略（Tactics）： 策略定义了将当前证明义务分解为一组更简单子目标的方式，从而逐步完成整个证明。从概念上看，一个策略 t 可以视为一种状态转移函数：

$t \in S \times I \rightarrow S′$

其中，S 表示一个目标，I 表示可能存在的参数集合，S′ 表示执行该策略后得到的一组目标。举例来说，图 1 第 4 行的策略 induction n 指示 Coq 对局部上下文中的自然数 n 进行数学归纳。执行该策略会将图 2b 的证明状态转化为图 2c，其中包含两个子目标：(1) 基本情况，即 n = 0；(2) 归纳情况，即 n 为任意自然数。需要注意的是，当存在多个子目标时，Coq 仅显示第一个目标的局部上下文。值得强调的是，若策略被错误应用，例如目标形式不匹配或参数错误，则该策略可能会失败。此时，Coq 会将失败信息反馈给用户。

证明（Proofs）： 一个定理的证明由一系列策略组成，这些策略逐步将初始目标（即定理陈述）转化为子目标，直至全部解决。证明的起始与结束分别由 Proof 和 Qed 命令标识（对应图 1 的第 2 行与第 11 行）。Qed 命令会触发 Coq 内核检查是否仍存在未完成的证明义务。若全部义务均已解决，Coq 将以成功状态退出证明模式，并将该定理加入全局上下文。

我们现在通过图 1 中的 add_comm 定理来进一步说明这些概念。在证明开始时（第 2 行），证明状态由一个目标组成，该目标对应顶层的定理陈述（见图 2a）。在第 3 行，策略 intros n m 指示 Coq 将全称量化变量 n 和 m 引入局部上下文（图 2b）。随后，第 4 行中提到的 induction n 策略对 n 进行数学归纳，从而生成两个子目标，分别对应基本情形与归纳情形（图 2c）。接下来，我们使用子目标标记符号 “-”（第 5 行）开始证明第一个子目标，该符号既标记了子目标证明的起始，也使 Coq 仅显示该子目标（图 2d）。在完成第一个子目标后，我们以相同的标记符号（第 7 行）进入下一个子目标的证明。这些符号在组织证明结构时十分重要，它们确保 Coq 在进入下一个子目标前，必须先完成当前子目标的证明。

我们通过调用 auto 策略（第 6 行）解决基本情形（图 2d），该策略依赖符号化的自动证明方法来消解简单目标。随后进入第二个子目标，即归纳情形。需要特别指出的是，该目标的局部上下文中包含归纳假设。我们首先使用 simpl 策略（第 8 行），它通过对加法运算符“+”进行化简来简化目标（图 2f）。之后使用 rewrite IHn 策略（第 9 行），将归纳假设 IHn 的左侧替换为右侧，从而改写当前目标（图 2g）。最后，我们调用 Coq 标准库中一个已被证明的定理 plus_n_Sm：

$\forall n\ m : nat,\ 1 + (n + m) = n + (1 + m)$

该定理表明，在和式 n + m 上加 1，与将 n 加到 m + 1 上是等价的。对于形如 A ⇒ B 的定理，如果其结论 B 与当前证明义务相匹配，则可将该定理应用于目标，从而得到对应于其前提 A 的新目标。在本例中，策略 apply plus_n_Sm 直接解决了当前目标，因为该定理的结论与目标完全一致，且该定理没有任何前提条件。此时所有目标均已解决，证明完成，并最终通过 Qed 命令结束 add_comm 的证明。

2.2 Hammers

为了简化证明构造，Coq 内置了许多成熟的自动化证明策略（例如 auto）。这些策略要么完全解决当前目标，要么在失败时保持目标不变。在这些策略中，hammers 是一种功能极其强大的策略，它们通过调用外部自动定理证明器（ATP）来处理目标，典型的 ATP 包括 Vampire、CVC5、E 和 Z3。许多流行的交互式定理证明器（ITP）都配备了 hammers，例如 Coq 的 CoqHammer，Isabelle 的 SledgeHammer，以及 HOL Light 的 HOLyHammer。

从整体上看，hammers 的工作流程如下：首先将当前目标编码为外部 ATP 可处理的形式，通常为一阶逻辑公式。这一步骤是必要的，因为 ITP 所支持的逻辑通常比大多数 ATP 更加丰富（如高阶逻辑）。为了使底层 ATP 能够利用先前已证明的定理，需要从全局上下文中选取一部分定理与当前目标一起进行编码，而如何选取这些相关定理的过程通常称为前提选择。早期的 hammers 依赖启发式方法完成前提选择，而现代 hammers 则通常使用机器学习算法来提高选择的准确性。在目标与所选定理完成编码后，hammers 调用 ATP 进行求解；若求解成功，ATP 所生成的证明会被翻译为 ITP 可理解的形式。

hammers 通常通过调用特定的策略来使用。例如，CoqHammer 提供了 hammer、hfcrush 和 qsimpl 等策略，它们分别利用不同的自动化方法来证明目标。尽管 hammers 功能强大，但它们仅覆盖 ITP 可用推理的一部分。例如，它们通常不执行数学归纳，从而限制了其直接证明复杂定理的能力。尽管如此，它们在精确解决小规模子目标方面依然非常有效。例如，hammer 策略能够完全解决图 2d 与图 2e 中的目标，而 Coq 的 auto 策略仅能解决第一个目标。

3 形成性研究

虽然大语言模型（LLMs）此前已被用于生成 Coq 证明，但其效果并不理想。为了理解这一问题的根本原因，我们开展了一项形成性研究，旨在识别 LLM 在生成证明脚本时常见的错误。在该研究中，我们评估了 GPT-3.5 在证明 Verdi 项目中 579 个定理时的表现。Verdi 是一个分布式系统验证项目，也曾在其他研究中被使用。

我们基于广泛应用的检索增强生成（RAG）方法精心设计了提示（prompt）。该提示同样被 PALM 使用，并将在第 4.2 节和第 4.3 节中详细描述。我们调用了当时最新版本的 GPT-3.5-turbo-1106 API，采用默认的解码温度。对于每个定理，我们仅采样一个证明脚本，并在 Coq 中运行生成的证明，记录第一个出现的错误信息。

最终我们收集了共计 520 个错误，并基于扎根理论和开放编码方法进行了深入的人工分析。首先，第一作者标注了 100 个错误并提出初步分类方案；随后，他与最后一作者在两次会议中讨论并改进了标签和分类；之后，第一作者根据改进后的标签和分类对其余错误进行标注与归类。最后，全体作者共同讨论并最终确定分类，其中第二作者（定理证明领域专家）提供的见解进一步提升了分类体系。整个过程约耗时 52 人工小时。最终我们将 520 个错误划分为七类，如表 1 所示。

错误类型	出现次数	占比 (%)
错误的定理应用	258	49.6
非法引用	79	15.2
错误的重写	61	11.7
冗余引入	56	10.8
策略误用	44	8.5
子目标标记误用	19	3.7
其他错误	3	0.6
合计	520	100

1. 错误的定理应用（49.6%）： 当存在一个形如 H: A ⇒ B 的定理或假设，且当前目标为 B 时，可以使用 apply H 策略将目标替换为前提 A。该策略要求 H 的结论与目标完全匹配。如果尝试应用一个结论与目标不匹配的定理或假设，策略会失败。例如，在图 3 中，证明状态中存在假设 H: m = n，但目标为 n = m，两者不匹配，因此应用 H 会失败，并返回错误信息：“Unable to unify ‘m=n’ with ‘n=m’.”

2. 非法引用（15.2%）： LLM 可能生成错误的引用，如引用不存在于局部上下文的假设，或引用在环境中找不到的定理。这是一种典型的“幻觉”现象。

3. 错误的重写（11.7%）： 给定一个等式 Heq，rewrite Heq 策略会将目标中出现的 Heq 左侧项替换为右侧项。当被用于重写的定理或假设的左侧在目标中没有任何匹配子项时，便会出错。例如，在图 5 的证明状态中，rewrite H2 会失败，并返回错误信息：“Found no subterm matching ‘b’ in the current goal.”

4. 冗余引入（10.8%）： intros 策略用于将全称量化的变量和假设引入局部上下文。但在某些情况下，LLM 生成的证明会错误地使用 intros 来引入一个已经存在于上下文中的名称，或者在没有任何可引入对象时仍然调用 intros。

5. 策略误用（8.5%）： 某些策略只能作用于特定类型的参数。如果参数不满足要求，则会导致错误。例如，destruct 与 induction 只能应用于归纳数据类型（如自然数），若作用于非归纳类型，则会失败并报错 “Not an inductive product”。相反，unfold 策略不能作用于归纳类型，否则会报错 “Cannot turn inductive into an evaluable reference”。其他内置策略也可能被误用。例如，reflexivity 在目标不是两个等价项的相等式时会失败，而 contradiction 在局部上下文中不存在矛盾时也会失败。

6. 子目标标记误用（3.7%）： LLM 可能在两个方面误用子目标标记：（1）在当前子目标尚未完成时，就尝试进入下一个目标；（2）使用了错误的标记符号来聚焦目标。例如，在图 6 的第一个错误证明中，第 6 行的第二个标记应为 “-” 而非 “+”，导致错误 “Wrong bullet +: Expecting -.”；在第二个错误证明中，第 12 行的 simpl 未能完全解决第一个子目标，继续进入第二个子目标会触发错误 “Wrong bullet -: Current bullet - is not finished.”

7. 其他错误（0.6%）： 少数错误不属于上述类别。例如，LLM 可能生成特殊命令 Abort，该命令会在证明尚未完成时直接终止证明，且不会抛出错误。

这项形成性研究的一个关键发现是：LLM 在生成证明脚本时，虽然经常能够捕捉正确的高层次结构，但在处理细粒度的低层细节时往往表现不足，而这正是 hammers 擅长的部分。例如，GPT-3.5 通常知道在何时使用 induction 策略将定理分解为子目标，但经常无法生成正确的策略序列来逐一证明这些子目标。另一方面，CoqHammer 借助 ATP 在解决这些子目标时表现出色。此外，我们发现许多证明生成错误相对容易修复，例如通过基于规则的转换，而无需从头重新生成整个证明。例如，子目标标记误用的两类错误，都可以通过系统性地插入正确的标记来修复。

4 方法

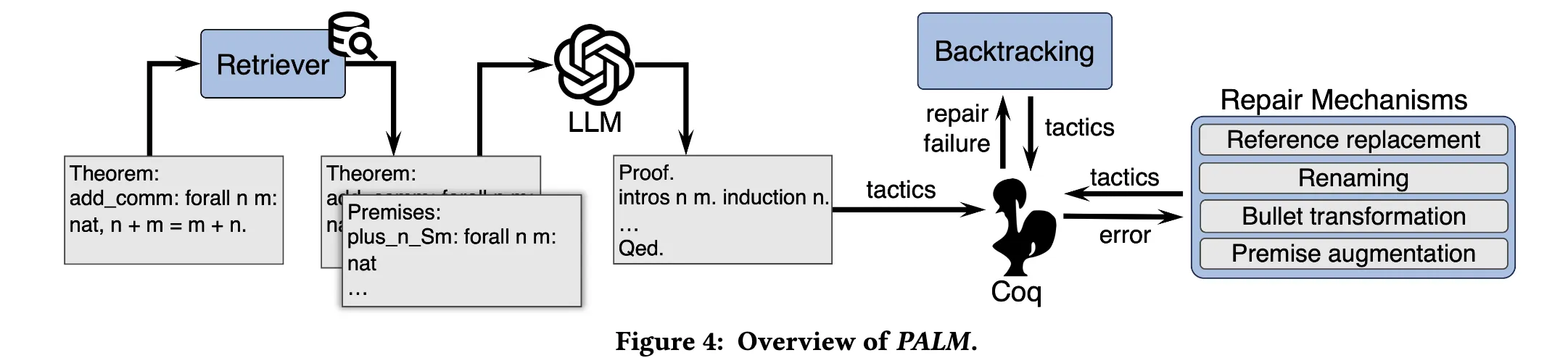
在形成性研究的启发下，我们提出 PALM，一种结合大语言模型（LLMs）与符号方法的自动化证明方法。图 4 展示了 PALM 的整体框架。PALM 包含三个核心组成部分：（1）基于检索增强的证明生成方法；（2）一组修复机制；（3）回溯过程。

4.1 总体算法

算法 1 描述了 PALM 所采用的“生成-修复”流程。其输入为一个定理陈述 t、环境 env 和语言模型 LM。首先，PALM 使用第 4.2 节介绍的检索增强生成（RAG）方法，从 env 中检索与 t 相关的前提（第 3 行）。接着，PALM 使用 t 及所选前提构造提示（prompt）（第 4 行），并调用 LM 生成初始证明脚本（第 5 行）。随后，PALM 在 Coq 中依次执行这些策略（第 6–15 行）。

如果执行过程中出现错误，PALM 会调用一组修复机制（第 9 行），依据错误信息、触发错误的策略以及当前证明状态来尝试修复。如果 PALM 无法修复错误，则会触发回溯过程（第 11 行），该过程在算法 2 中描述，其核心思想是利用 CoqHammer 修复先前的证明。若在所有策略执行完毕后不再存在未解决的目标，则证明成功完成（第 16 行）。